Splitsen tot 10: knelpunt 2

Splitsen is een belangrijke rekenvaardigheid. De meeste rekenmethodes bieden in groep 3 en 4 veel activiteiten aan op het gebied van splitsen. De beelddenkers in de klas leggen echter geen automatische verbanden tussen geleerde vaardigheden. Er ontstaan zogenaamde ‘eilandjes van kennis’, die afzonderlijk van elkaar wellicht beheerst worden, maar waarvan kinderen niet begrijpen wat ze met elkaar te maken hebben. In deze blog lees je meer over knelpunt 2 bij het splitsen en hoe je verschillende schema’s op elkaar kunt laten aansluiten.

Knelpunt 2: gebruik van verschillende schema’s

We gebruiken in het onderwijs vaak verschillende manieren om een splitsing weer te geven. Zo knutselen we zelf splitshuisjes in elkaar, maken we gebruik van de schema’s uit de methode en gaan we aan de slag met bewegend leren. Om de kinderen te helpen, werken we in het begin meestal met één schema voor één splitsing.

Uiteindelijk worden deze schema’s samengevoegd tot ‘de tabel’, waarin alle splitsingen van een getal komen te staan. Dat een tabel eigenlijk een samenvoeging van meerdere schema’s is, kan de zwakke rekenaars ontgaan.

Een (tussen)oplossing

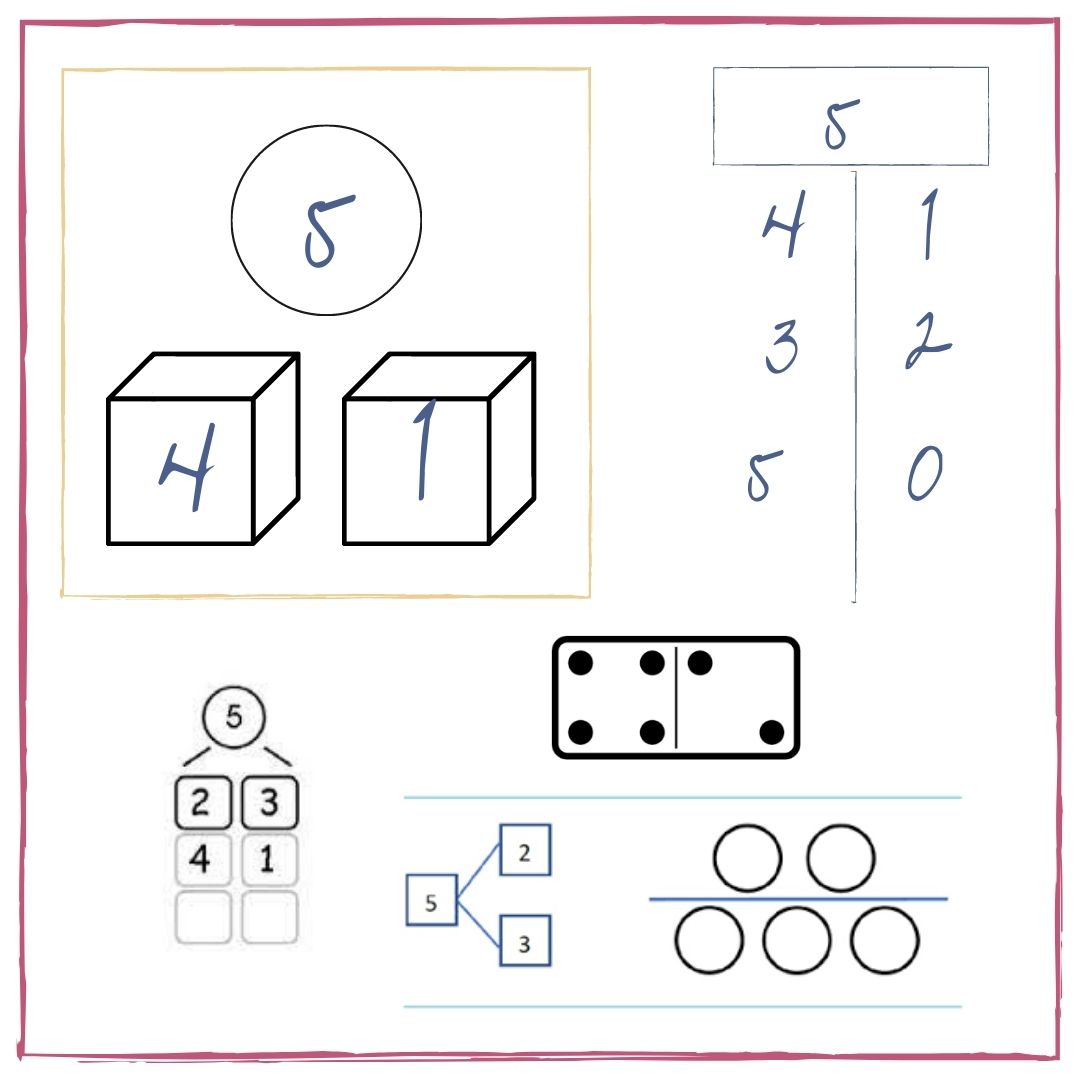
Zorg ervoor dat alle schema’s en tabellen regelmatig samenkomen. Op deze wijze integreren de ‘eilandjes van kennis’. Zo start ik mijn les vaak op met een splitshandeling (Lego-poppetjes verdelen over twee doosjes). Daar koppel ik een schema aan vast (een cirkel met het getal dat gesplitst wordt met twee vierkanten eronder) die de kinderen invullen aan de hand van hun handeling. Dit schema koppel ik aan de les die we doen uit de methode ‘de Splitslijn’. In deze methode worden het handelen (kleuren) en de tabel al aan elkaar gekoppeld.

In een later stadium voeg ik daar volgens de methodiek sommen aan toe. Dit is het laatste niveau vanuit de visie waarbij je werkt met handelingsniveaus tijdens het rekenonderwijs.

Een veelvoorkomende fout

Zoals in blog 1 van deze reeks is vermeld, maken kinderen die een schema invullen nog al eens de fout dat ze de splitsing verwarren met de optelling. Een kind vult dan bijvoorbeeld 14 in (want 10 en 4 is 14). In dit geval heeft het kind duidelijk niet begrepen, dat het bij splitsen gaat om een gegeven hoeveelheid die je in twee delen deelt.

Ook zie ik dat veel kinderen in de war raken als je het getal NIET in twee even grote delen mag verdelen (8 is 4 en 4, maar ook 3 en 5).

Een (tussen)oplossing

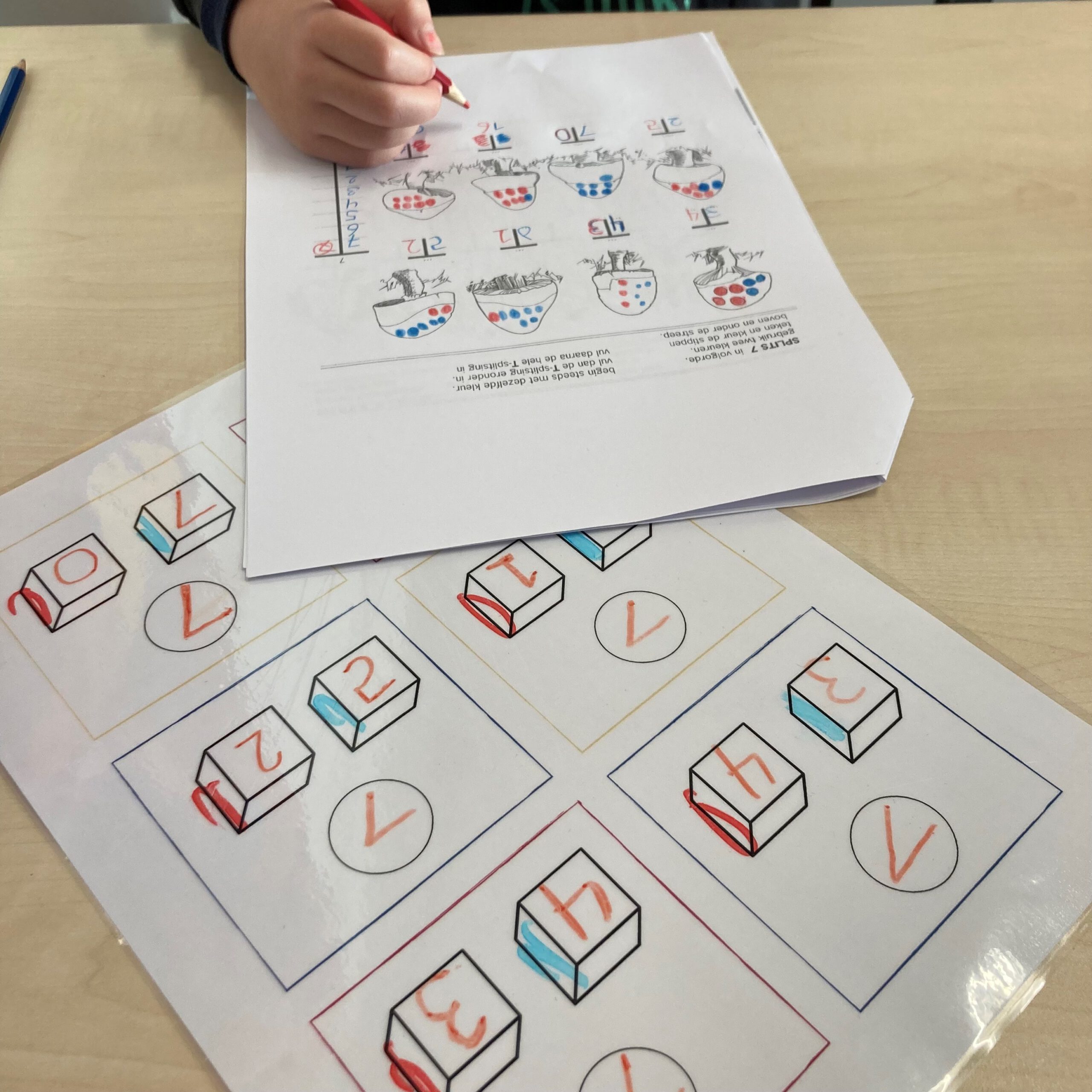
Zeker voor beelddenkers en leerlingen uit het s(b)o geldt, dat zij eerst moeten ervaren wat er eigenlijk gebeurt bij een splitsing voordat wordt gewerkt met schema’s en modellen. Sla de stap van het ervaren dan ook niet te snel over. Neem deze ervaring juist mee tijdens het leggen van de link naar de schema’s en modellen. In de methode ‘de Splitslijn’ wordt deze stap als volgt aangeboden:

Op een afgeschermde pagina op deze website vind je alle Splitslijn-bestanden. Heb je hier interesse om deze bestanden te downloaden, mail me gerust. Houd de website in de gaten, het volgende knelpunt volgt snel.

Liefs,
Tineke