Splitsen tot 10: knelpunt 1

Splitsen is een belangrijke rekenvaardigheid. De meeste rekenmethodes bieden in groep 3 en 4 veel activiteiten aan op het gebied van splitsen. De beelddenkers in je klas leggen echter geen automatische verbanden tussen geleerde vaardigheden. Er ontstaan zogenaamde ‘eilandjes van kennis’ die afzonderlijk van elkaar wellicht beheerst worden, maar waarvan kinderen niet begrijpen wat ze met elkaar te maken hebben. Lees meer over dit knelpunt en hoe je de ‘eilandjes van kennis’ kunt integreren tot een geheel.

Methodes beginnen op een te hoog abstractieniveau

Kinderen die in beelden denken, hebben over het algemeen niet zo veel op met het abstractieniveau dat ze tegenkomen tijdens de rekenlessen. Abstract taalgebruik zorgt ervoor dat ze geen beelden kunnen oproepen en de aangeboden stof moeizaam of niet beklijft.

Kijken we naar de gemiddelde rekenmethode, dan zien we dat deze groep 3 en 4 veel activiteiten aanbieden op het gebied van splitsen. Het probleem hierbij is echter dat deze meestal op een behoorlijk hoog niveau van abstractie beginnen. Vaak moeten er schema’s ingevuld worden. Denk maar aan de splitshuisjes en onderstaande oefeningen:

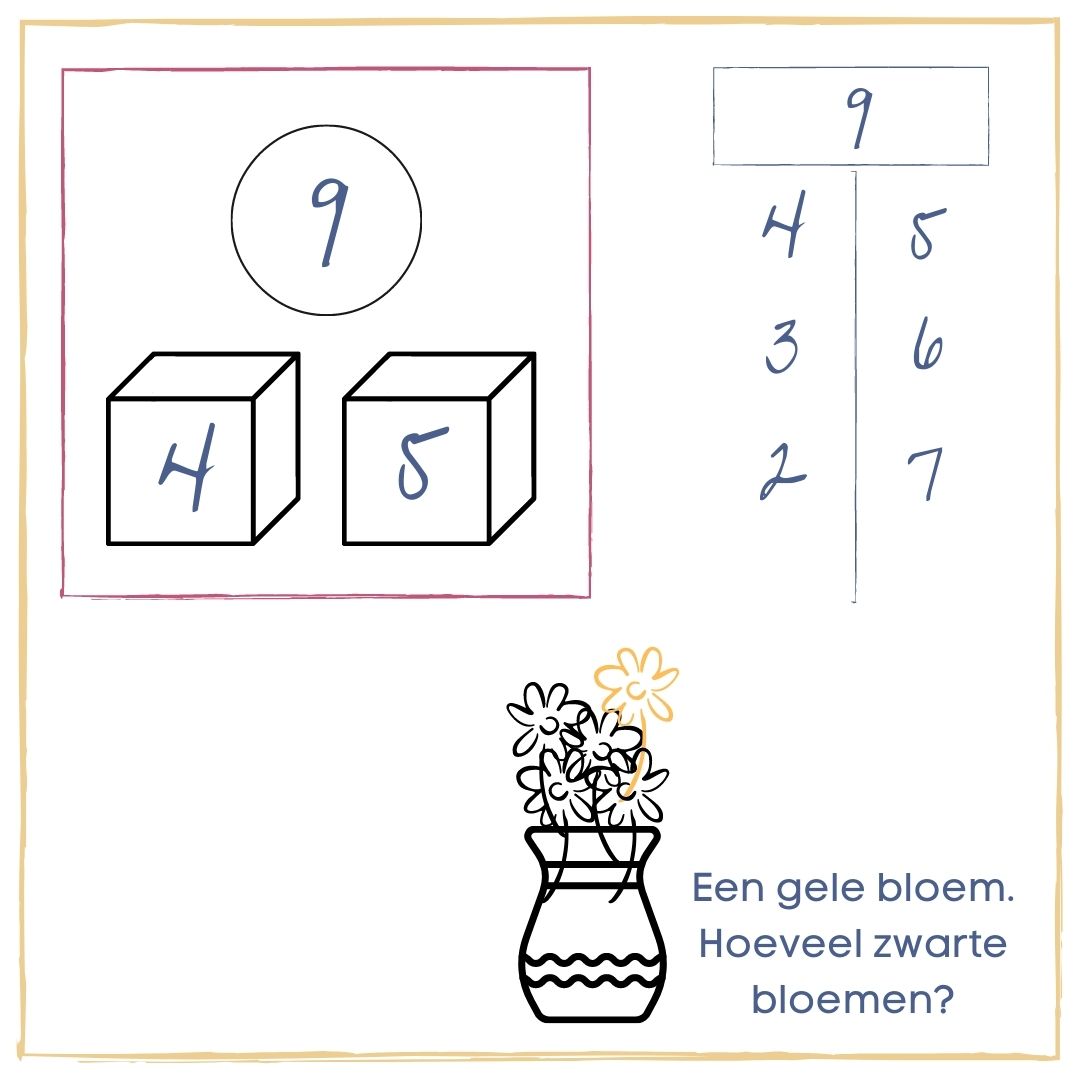
Soms zijn er wel verkennende activiteiten aan vooraf gegaan of erop volgend, maar voor veel beelddenkers is niet duidelijk dat hier dezelfde vaardigheid wordt gevraagd. Ook leerlingen in het s(b)o hebben vaak moeite om deze koppeling te maken. Doordat ze deze koppeling niet maken, kan er een los ‘eilandje’ ontstaan, dat niets met het voorgaande of erop volgende te maken heeft.

Een (tussen)oplossing

Deze kinderen hebben het nodig dat verbanden tussen de activiteiten nadrukkelijk worden gelegd. Dat kan bijvoorbeeld door een overgangsfase te creëren waarin verschillende schema’s een tijdje naast elkaar aan bod komen, het liefst op hetzelfde werkblad. De kinderen wordt gevraagd naar de overeenkomsten en de verschillen.

Een veelvoorkomende fout

Kinderen die een schema invullen, maken nog al eens de fout dat ze de splitsing verwarren met de optelling. Een kind vult dan bijvoorbeeld 14 in (want 10 en 4 is 14). In dit geval heeft het kind duidelijk niet begrepen dat het bij splitsen gaat om een gegeven hoeveelheid die je in twee delen deelt.

Zeker voor beelddenker en leerlingen uit het s(b)o geldt, dat zij eerst moeten ervaren wat er eigenlijk gebeurt bij een splitsing voordat wordt gewerkt met schema’s en modellen.

Houd de website in de gaten, de volgende knelpunten volgen binnenkort.

Liefs,
Tineke